Aljabar Linier Matriks
Hay gan, kali ini saya akan menuliskan artikel saya yang kedua setelah yang pertama saya posting soal introduction atau pengenalan, tentunya ini masih dalam materi ilmu komputasi hanyalah lanjutan yang berjudul ALJABAR LINIER MATRIKS.
oke, seperti biasa saya akan mendefinisikan terlebih dahulu apa itu aljabar linier matriks ?
Matriks
•Matriks merupakan bilangan-bilangan yang berbentuk atas baris-baris dan kolom-kolom.
•Masing-masing bilangan dalam matriks disebut entri atau elemen.
•Ordo (ukuran) matriks adalah jumlah baris kali jumlah kolom.
Matriks persegi
Matriks persegi (bujursangkar) adalah matriks yang jumlah baris dan jumlah kolomnya sama.
Trace dari matriks adalah jumlahan elemen-elemen diagonal utama.
Matriksnol dan identitas
Matriks Nol adalah matriks yang semua elemennya nol
Matriks identitas adalah matriks persegi yang elemen diagonal utamanya 1 dan elemen lainnya 0
Kesamaan dua matriks
Dua matriks sama jika ukuran sama dan setiap entri yang bersesuaian sama.
Penjumlahan dan Pengurangan Matriks
•Contoh
•Syarat agar dua matriks dapat dijumlahkan : ordo matriks tersebut sama
Hasil perkalian nilai skalar dengan matriks
•Contoh :
Apa hubungan H dengan A?
Perkalian Matriks
Definisi :
Jika A = [aij] berukuran m x r , dan B = [bij] berukuran r x n, maka matriks hasil kali A dan B, yaitu C = AB mempunyai elemen-elemen yang didefinisikan sebagai berikut :
Syarat matriks bisa di kalikan adalah Jumlah kolom matriks A
sama dengan jumlah baris matriks B
Perkalian Matriks
Perkalian matriks (lanjutan)
1. Diberikan A dan B, AB dan BA terdefinisi. Apa kesimpulanmu ?
2. AB= O matriks nol, apakah salah satu dari A atau B pasti matriks nol ?
#AB matriks nol, belum tentu A atau B matriks nol#
Perpangkatan Matriks
Contoh:

Penyajian Sistem Persamaan Linier dalam persamaan matriks
•SPL dalam bentuk :
•dapat disajikan dalam bentuk persamaan matriks:
Contoh : Penyajian SPL dengan persamaan matriks

Perkalian dengan matriks identitas

Inverse matriks
B adalahinverse darimatriksA, jikaAB = BA = I (matriksidentitas), ditulisB = A-1
Inverse matriks 2x2
#Jikaa d – b c = 0 maka A TIDAK mempunyai inverse.#
Matriks Simetri Matriks A disebut simetris jika dan hanya jika A = A'
Sifat-sifat transpose matriks
1.Transpose dari A transpose adalah A: (A')'=A
Matrik sortogonal
Demikianlah artikel yang saya buat dengan apa adanya, hehehe :D
yang saya ambil dari modul yang diberikan oleh dosen, apa bila artikel ini banyak kekurangan saya admin memohon maaf kepada pembaca, karena semua ciptaan itu tidak ada yang sempurna .
terima kasih sudah berkunjung, dan menyempatkan waktu anda untuk mempelajari materi tersebut.
apa bila ada saran atau kritikan silahkan tinggalkan dikolom komen, terimakasih dan jangan bosan2 untuk berkunjung, hehehe :D
yang saya ambil dari modul yang diberikan oleh dosen, apa bila artikel ini banyak kekurangan saya admin memohon maaf kepada pembaca, karena semua ciptaan itu tidak ada yang sempurna .
terima kasih sudah berkunjung, dan menyempatkan waktu anda untuk mempelajari materi tersebut.
apa bila ada saran atau kritikan silahkan tinggalkan dikolom komen, terimakasih dan jangan bosan2 untuk berkunjung, hehehe :D
Semoga artikel Aljabar Linier Matriks bermanfaat bagi Anda. Jika kamu suka dengan artikel Aljabar Linier Matriks ini, like dan bagikan ketemanmu.










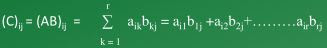

















Post a Comment